当サイトはアフィリエイト広告を利用してます
余弦定理による距離の算出
下の図で、BCの距離を知りたい場合に、余弦定理が使用できる。
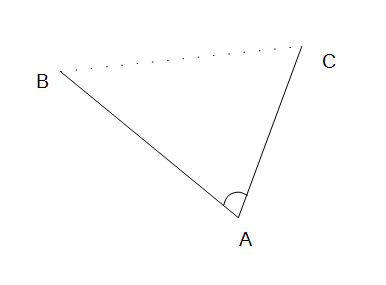
BCの距離が直接測れる場合は、わざわざ面倒な計算をしなくても良いですね。ただ、実際には、BCを直接測定できない、という場合もあるでしょう。
BC間に池があったり、大きな建物があったり、といった場合です。そのような場合に、余弦定理が役立ちます。
角が90度となるとき、三平方の定理(ピタゴラスの定理)が成立します。
三平方の定理は、AB x AB + AC x AC = BC x BC で、角Aがちょうど90度の場合。
また、1つの辺とその両端の角が既知の場合に残りの辺の長さを求めるには正弦定理が有効です。
更新日:

↑このページへのリンクです。コピペしてご利用ください。