当サイトはアフィリエイト広告を利用してます
正弦定理による線分の長さの計算
三角形の合同条件の一つに、「一つの辺の長さとその両端の角の大きさが等しい」というものがあります。これはすなわち、
『「一つの辺の長さとその両端の角の大きさ」が既知であれば、残りの二つの辺の長さを確定できる』
ということでもあります。現実的な応用としては、たとえば、一つの辺の長さとその両端の角の大きさを測定することで残りの二つの辺の長さを知ることができる、があります。
では実際に、一つの辺の長さとその両端の角の大きさから、残りの二つの辺の長さを求めてみましょう。
計算には、正弦定理を使用します。
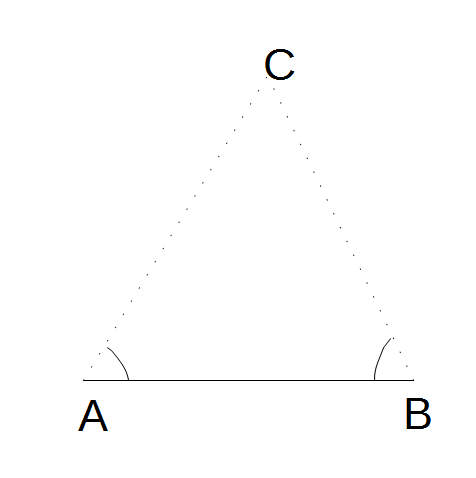
三角形の内角の和は180度なので、角Aと角Bの角度が分かると、角Cの角度も決まります。
辺AB = 2×R×sin(角C)
から、R(外接円の半径)が計算できます。
辺AC = 2×R×sin(角B)
辺BC = 2×R×sin(角A)
から、AC、BCの長さを計算できます。
直接測量できない場合に便利
直接ACやBCを測量できるのであれば、三角関数で計算しなくてもよいですね。しかし、常に直接測量できるとは限りません。ACの途中に民家があったり、交通量の多い道路があったりした場合はどうでしょうか。このような場合は、ACの長さを直接測量するよりも三角関数で求めたほうがよいでしょう。
更新日:

↑このページへのリンクです。コピペしてご利用ください。